Answer:
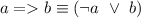
Explanation:
You can understand the statement from many perspectives, but in terms of proposition logic it is best to understand it as "negation of a" or " b" in mathematical terms is written like this
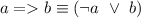
You can show that they are logically equivalent because they have the same truth table.