Complete Question
Assume that when adults with smartphones are randomly selected 42% use them in meetings or classes if 15 adult smartphones are randomly selected, find the probability that "fewer" than 4 of them use their smartphones
Answer:
The probability is
![P[X < 4]= 0.00314](https://img.qammunity.org/2021/formulas/mathematics/college/h9wagx4z2fsgsdslo06rdupy1lxy6mjoyg.png)
Explanation:
From the question we are told that
The proportion of those that use smartphone in meeting and classes is p = 0.42
The sample size is

The proportion of those that don't use smartphone in meeting and classes is
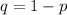
=>
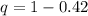
=>
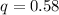
Now from the question we can deduce that the usage of the smartphone is having a binomial distribution since there is only two outcome
So the probability that "fewer" than 4 of them use their smartphones is mathematically evaluated as
![P[X < 4 ] = P[X = 0] + P[X = 1] +P[X = 2] +P[X = 3]](https://img.qammunity.org/2021/formulas/mathematics/college/ll3fb9ow7be6lcf0spwom6ldztr41qx6lj.png) =
=
=>
![P[X < 4] = [ \left 15} \atop {0}} \right. ] p^(15-0) * q^0 + [ \left 15} \atop {1}} \right. ] p^(15-1 )* q^1 + [ \left 15} \atop {2}} \right. ] p^(15-2 )* q^2 + [ \left 15} \atop {3}} \right. ] p^(15-3 )* q^3](https://img.qammunity.org/2021/formulas/mathematics/college/1f4afjl065p7y5u9w7jt9j62508chk4gth.png)
Where
![[\left 15} \atop {0}} \right. ]](https://img.qammunity.org/2021/formulas/mathematics/college/x4yvhkh8nzl7z9ut5x14a4vf2pnvi916l1.png) implies 15 combination 0 which has a value of 1 this is obtained using a scientific calculator
implies 15 combination 0 which has a value of 1 this is obtained using a scientific calculator
So for the rest of the equation we will be making use of a scientific calculator to obtain the combinations
![P[X < 4] = 1 * ^(15) * q^0 + 15 * p^(14 )* q^1 + 105 * p^(13 )* q^2 + 455 * p^(12 )* q^3](https://img.qammunity.org/2021/formulas/mathematics/college/q10kqz7i1v38uipzi3hc49nhd7yvxbp8xk.png)
substituting values
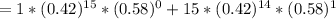
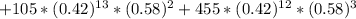
=>
![P[X < 4]= 0.00314](https://img.qammunity.org/2021/formulas/mathematics/college/h9wagx4z2fsgsdslo06rdupy1lxy6mjoyg.png)