Question

PLEASE HELP NOW --- >N is a 2-digit even number. If the last two digits of N^2 is the same as N, what is the sum of digits of N?

Answer 1

76.

Explanation:

It is given that N is a 2-digit number.

Last two digits of N^2 is the same as N.

We know that, a number is even if it ends with 0,2,4,6,8.

`2^2=4,4^2=16,6^2=36,8^2=64`

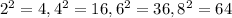
If 0 is in end then we get two zeros in the square of that number.

It is clear that, number should ends with 6 to get the same number at the end.

`16^2=256`

`26^2=676`

`36^2=1296`

`46^2=2116`

`56^2=3136`

`66^2=4356`

`76^2=5776`

`86^2=7396`

`96^2=9216`

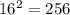
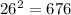
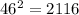
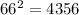
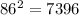
It is clear that last two digits of (76)^2 is the same as 76.

Therefore, the required number is 76.