Answer:
The concentrations are: [K⁺] = 1.2 M, [OH⁻] = 0.016 M, [CO₃²⁻] = 1.18 M and [H⁺] = 6.25x10⁻¹³ M.
Step-by-step explanation:
The dissociation equation of K₂CO₃ in water is:
K₂CO₃(aq) ⇄ K⁺(aq) + CO₃²⁻(aq) (1)
Also, the CO₃²⁻ will react with water as follows:
CO₃²⁻(aq) + H₂O(l) ⇄ HCO₃⁻(aq) + OH⁻(aq) (2)
The constant of the reaction (2) is:
![Kb = ([OH^(-)][HCO_(3)^(-)])/([CO_(3)^(-2)]) = 2.08 \cdot 10^(-4)](https://img.qammunity.org/2021/formulas/chemistry/college/r26o7p25ih7i3wzf0jjx9foj0o00bp3rr8.png)
The solution of K₂CO₃ is 1.2 M, and since the mole ratio of K₂CO₃ with K⁺ and CO₃²⁻ is 1:1, then we have:
![[K_(2)CO_(3)] = [K^(+)] = [CO_(3)^(-2)] = 1.2 M](https://img.qammunity.org/2021/formulas/chemistry/college/mvwwsbqdayd7a5z7gtxpqxu3ahfg6vjcag.png)
Now, from equation (2) we have:
CO₃²⁻(aq) + H₂O(l) ⇄ HCO₃⁻(aq) + OH⁻(aq) (3)
1.2 - x x x
![2.08 \cdot 10^(-4) = ([OH^(-)][HCO_(3)^(-)])/([CO_(3)^(-2)])](https://img.qammunity.org/2021/formulas/chemistry/college/puk23jkyi58tielftqu33xjaza3yn225ai.png)
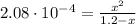
 (4)
(4)
By solving equation (4) for x we have:
x = 0.016 M = [HCO₃⁻] = [OH⁻]
Hence, the CO₃²⁻ concentration is:
[CO₃²⁻] = 1.2 M - 0.016 M = 1.18 M
Finally, the concentration of [H⁺] is:
![[H^(+)][OH^(-)] = 10^(-14)](https://img.qammunity.org/2021/formulas/chemistry/middle-school/un2kbfu4nv4cbgqa93fshl57zk5lo34wo0.png)
![[H^(+)] = (10^(-14))/([OH^(-)]) = (10^(-14))/(0.016) = 6.25 \cdot 10^(-13) M](https://img.qammunity.org/2021/formulas/chemistry/college/yikypr9yxv0246zafam447nsknd8fjoi79.png)
Therefore, the concentrations are: [K⁺] = 1.2 M, [OH⁻] = 0.016 M, [CO₃²⁻] = 1.18 M and [H⁺] = 6.25x10⁻¹³ M.
I hope it helps you!