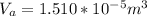Question

At 30.0 m below the surface of the sea (density = 1 025 kg/m3), where the temperature is 5.00°C, a diver exhales an air bubble having a volume of 0.95 cm3. If the surface temperature of the sea is 20.0°C, what is the volume of the bubble just before it breaks the surface?

Answer 1

The volume is
`V_a = 1.510 *10^(-5) m^3`

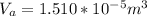
Step-by-step explanation:

From the question we are told that

The depth below the see is
`d_1 = 30.0 \ m`

The density of the sea is
`\rho_s = 1025 \ kg /m^3`

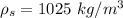
The temperature at this level is
`T_d = 5.00 ^oC = 278 \ K`

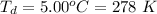
The volume of the air bubble at this depth is
`V_d = 0.95 \ cm^3 = 0.95 *0^(-6)\ m`

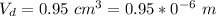
The temperature at the surface is
`T_a = 20^oC =293\ K`

Generally the pressure at the given depth is mathematically evaluated as

`P_d = P_o + \rho_s * g * d`

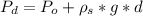
Where
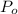`P_o` is the atmospheric pressure with a constant value

`P_o = 1.013 *10^(5) \ Pa`

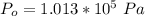
substituting values

`P_d = 1.013 * 10^(5) * + (1025 * 9.8 * 30 )`

`P_d = 4.02650 * 10^(5) \ Pa`

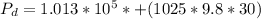
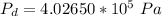
According to the combined gas law

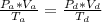
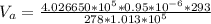
`(P_a * V_a )/(T_a ) = (P_d * V_d )/(T_d )`

=>
`V_a = (4.026650 *10^(5) * 0.95 *10^(-6) * 293 )/(278 * 1.013*10^(5) )`

=>
`V_a = 1.510 *10^(-5) m^3`