Answer:
Reject the null hypothesis. There is sufficient evidence to conclude that the mean is less than 31%.
Explanation:
In this case we need to test whether the popular charity has expenses that are higher than other similar charities.
The hypothesis for the test can be defined as follows:
H₀: The popular charity has expenses that are higher than other similar charities, i.e. μ > 0.31.
Hₐ: The popular charity has expenses that are less than other similar charities, i.e. μ < 0.31.
As the population standard deviation is not known we will use a t-test for single mean.
Compute the sample mean and standard deviation as follows:
![\bar x=(1)/(n)\sum X=(1)/(10)\cdot[0.26+0.12+...+0.26]=0.238\\\\s= \sqrt{ \frac{ \sum{\left(x_i - \overline{X}\right)^2 }}{n-1} } = \sqrt{ ( 0.0674 )/( 10 - 1) } =0.08654\approx 0.087](https://img.qammunity.org/2021/formulas/mathematics/college/lo1xcqt8wm6mh8ku21elxd8kk72b8izrem.png)
Compute the test statistic value as follows:
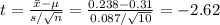
Thus, the test statistic value is -2.62.
Compute the p-value of the test as follows:
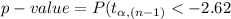
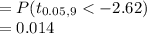
*Use a t-table.
Thus, the p-value of the test is 0.014.
Decision rule:
If the p-value of the test is less than the significance level then the null hypothesis will be rejected and vice-versa.
p-value = 0.014 < α = 0.05
The null hypothesis will be rejected at 5% level of significance.
Thus, concluding that there is sufficient evidence to conclude that the mean is less than 31%.