Question

A popular charity used 31% of its donations on expenses. An organizer for a rival charity wanted to quickly provide a donor with evidence that the popular charity has expenses that are higher than other similar charities. The organizer randomly selected 10 similar charities and examined their donations. The percentage of the expenses that those 10 charities spend on expenses is given below. Use a TI-83, TI-83 Plus, or TI-84 calculator to test whether the mean is less than 31% and then draw a conclusion in the context of the problem. Use α=0.05. 26 12 35 19 25 31 18 35 11 26 Select the correct answer below: Reject the null hypothesis. There is sufficient evidence to conclude that the mean is less than 31%. Reject the null hypothesis. There is insufficient evidence to conclude that the mean is less than 31%. Fail to reject the null hypothesis. There is sufficient evidence to conclude that the mean is less than 31%. Fail to reject the null hypothesis. There is insufficient evidence to conclude that the mean is less than 31%.

Answer 1

Reject the null hypothesis. There is sufficient evidence to conclude that the mean is less than 31%.

Explanation:

In this case we need to test whether the popular charity has expenses that are higher than other similar charities.

The hypothesis for the test can be defined as follows:

H₀: The popular charity has expenses that are higher than other similar charities, i.e. μ > 0.31.

Hₐ: The popular charity has expenses that are less than other similar charities, i.e. μ < 0.31.

As the population standard deviation is not known we will use a t-test for single mean.

Compute the sample mean and standard deviation as follows:

`\bar x=(1)/(n)\sum X=(1)/(10)\cdot[0.26+0.12+...+0.26]=0.238\\\\s= \sqrt{ \frac{ \sum{\left(x_i - \overline{X}\right)^2 }}{n-1} } = \sqrt{ ( 0.0674 )/( 10 - 1) } =0.08654\approx 0.087`

Compute the test statistic value as follows:

`t=(\bar x-\mu)/(s/√(n))=(0.238-0.31)/(0.087/√(10))=-2.62`

Thus, the test statistic value is -2.62.

Compute the p-value of the test as follows:

`p-value=P(t_(\alpha, (n-1))<-2.62}`

`=P(t_(0.05,9)<-2.62)\\=0.014`

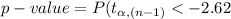
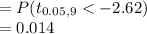
*Use a t-table.

Thus, the p-value of the test is 0.014.

Decision rule:

If the p-value of the test is less than the significance level then the null hypothesis will be rejected and vice-versa.

p-value = 0.014 < α = 0.05

The null hypothesis will be rejected at 5% level of significance.

Thus, concluding that there is sufficient evidence to conclude that the mean is less than 31%.