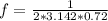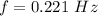Question

You have a resistor and a capacitor of unknown values. First, you charge the capacitor and discharge it through the resistor. By monitoring the capacitor voltage on an oscilloscope, you see that the voltage decays to half its initial value in 3.40 msms . You then use the resistor and capacitor to make a low-pass filter. What is the crossover frequency fcfc

Answer 1

The frequency is
`f = 0.221 \ Hz`

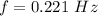
Step-by-step explanation:

From the question we are told that

The time taken for it to decay to half its original size is
`t = 3.40 \ ms = 3.40 *10^(-3) \ s`

Let the voltage of the capacitor when it is fully charged be
`V_o`

Then the voltage of the capacitor at time t is said to be
`V = (V_o)/(2)`

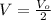
Now this voltage can be mathematical represented as

`V = V_o * e ^{-(t)/(RC) }`

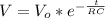
Where RC is the time constant

substituting values

`(V_o)/(2) = V_o * e ^{-(3.40 *10^(-3))/(RC) }`

`0.5 = e^{-(3.40 *10^(-3))/(RC) }`

`- (0.5)/(RC) = ln (0.5)`

`-(0.5)/(RC) = -0.6931`

`RC = 0.721`

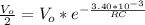
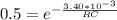
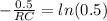
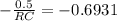
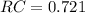
Generally the cross-over frequency for a low pass filter is mathematically represented as

`f = (1)/(2 \pi * RC )`

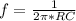
substituting values

`f = (1)/(2* 3.142 * 0.72 )`

`f = 0.221 \ Hz`