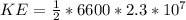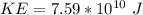Question

A satellite orbits a planet of unknown mass in a circular orbit of radius 2.3 x 104 km. The gravitational force on the satellite from the planet is 6600 N. What is the kinetic energy of the satellite

Answer 1

The kinetic energy is
`KE = 7.59 *10^(10) \ J`

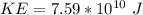
Step-by-step explanation:

From the question we are told that

The radius of the orbit is
`r = 2.3 *10^(4) \ km = 2.3 *10^(7) \ m`

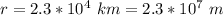
The gravitational force is
`F_g = 6600 \ N`

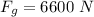
The kinetic energy of the satellite is mathematically represented as

`KE = (1)/(2) * mv^2`

where v is the speed of the satellite which is mathematically represented as

`v = \sqrt{(G M)/(r^2) }`

=>
`v^2 = (GM )/(r)`

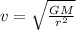
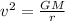
substituting this into the equation

`KE = ( 1)/(2) *(GMm)/(r)`

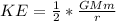
Now the gravitational force of the planet is mathematically represented as

`F_g = (GMm)/(r^2)`

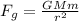
Where M is the mass of the planet and m is the mass of the satellite

Now looking at the formula for KE we see that we can represent it as

`KE = ( 1)/(2) *[(GMm)/(r^2)] * r`

=>
`KE = ( 1)/(2) *F_g * r`

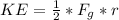
substituting values

`KE = ( 1)/(2) *6600 * 2.3*10^(7)`

`KE = 7.59 *10^(10) \ J`