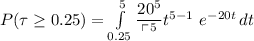Question

A web page is accessed at an average of 20 times an hour. Assume that waiting time until the next hit has an exponential distribution. (a.) Determine the rate parameter λ of the distribution of the time until the first hit? (b.) What is the expected time between hits? (c.) What is the probability that t

Answer 1

Explanation:

Given that :

A web page is accessed at an average of 20 times an hour.

Therefore:

a. he rate parameter λ of the distribution of the time until the first hit = 20

b. What is the expected time between hits?

Let consider E(Y) to be the expected time between the hits; Then :

E(Y) = 1/λ

E(Y) = 1/20

E(Y) = 0.05 hours

E(Y) = 3 minutes

(c.) What is the probability that there will be less than 5 hits in the first hour?

Let consider X which follows Poisson Distribution; Then,

P(X<5)
`\sim` G(∝=5, λ = 20)

For 5 hits ; the expected time will be :

Let 5 hits be X

E(X) = ∝/λ

E(X) = 5/20

E(X) =1/4

E(X) = 0.25 hour

E(X) = 15 minutes

From above ; we will see that it took 15 minutes to get 5 hits; then

`P(\tau \geq 0.25) = \int\limits^(\alpha)_(0.25) (\lambda^(\alpha))/(\ulcorner^(\alpha)) t^(a\pha-1) \ e^(-\lambda t) \, dt`

`P(\tau \geq 0.25) = \int\limits^(5)_(0.25) (20^(5))/(\ulcorner^(5)) t^(5-1) \ e^(-20 t) \, dt`

`\mathbf{P(\tau \geq 0.25) =0.4405}`