Answer:
Explanation:
To solve this problem you have to complete the square. To do that, set the quadratic equal to 0, then move the constant over to the other side. That's 2 steps in one, but they're simple ones:
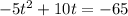
The first picky rule that completing the square has to follow is that the coefficient on the squared term has to be a 1. Ours is a -5, so we factor it out:
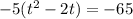 . Now it gets even pickier. To create a perfect square binomial on the left, we take half the linear term, square it, and add it in to both sides. Our linear term is a -2. Half of -2 is -1, and -1 squared is 1, so we add 1 into the set of parenthesis. BUT the -5 out front is a multiplier and refuses to be ignored. To offset the addition of the 1 inside the parenthesis, we have to multiply it by the -5 out front to get -5:
. Now it gets even pickier. To create a perfect square binomial on the left, we take half the linear term, square it, and add it in to both sides. Our linear term is a -2. Half of -2 is -1, and -1 squared is 1, so we add 1 into the set of parenthesis. BUT the -5 out front is a multiplier and refuses to be ignored. To offset the addition of the 1 inside the parenthesis, we have to multiply it by the -5 out front to get -5:
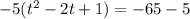
The perfect square binomial on the left side and simplifying the right:
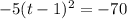 . Now we'll move the 70 over and set the quadratic back equal to y:
. Now we'll move the 70 over and set the quadratic back equal to y:
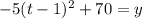
That's the quadratic in vertex form. The vertex here is (1, 70) which serves to answer 2 questions for us: the max height of the ball along with the time it was at that max height. For us, the ball reached a max height of 70 m after 1 second in its travels.
You could also do it the "calculus way" which is to find the derivative of the position function, which is
-10t + 10 = 0 and solve for t:
-10t = -10 so
t = 1. That's the time that the ball is at its highest point, and to find the highest point, sub that value in for t in the position function:
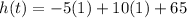 which comes to 70 m. I'm not sure what class you're taking so I did both! Calculus is way easier.
which comes to 70 m. I'm not sure what class you're taking so I did both! Calculus is way easier.