Question

Explain how you can determine the number of real number solutions of a system of equations in which one equation is linear and the other is quadratic–without graphing the system of equations.

Answer 1

To determine the number of real number solutions of as system of equations in which one equation is linear and the other is quadratic

1) Given that there are two variables, x and y as an example, we make y the subject of the equation of the linear equation and substitute the the expression for y in x into the quadratic equation

We simplify and check the number of real roots with the quadratic formula,
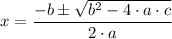`x = \frac{-b\pm \sqrt{b^(2)-4\cdot a\cdot c}}{2\cdot a}` for quadratic equations the form 0 = a·x² - b·x + c

Where b² > 4·a·c there are two possible solutions and when b² = 4·a·c equation there is only one solution.

Explanation:

Answer 2

Isolate one variable in the system of equations. Use substitution to create a one-variable equation. Then, set the quadratic equation equal to zero and find the discriminant. If the discriminant is negative, then there are no real number solutions. If the discriminant is zero, then there is one real number solution. If the discriminant is positive, then there are two real number solutions.

Explanation:

I just took the test on Edge 2020