Question

They can leave tonight by bus, or they can save two hours by leaving tomorrow morning and using the express train which travels 20 km/h faster than the bus. If the distance between South Central High and Calgary is 800 km, determine how long it will take to travel by bus, rounded to the nearest hour.

Answer 1

The bus will take 10 hours to travel from South Central High to Calgary.

Explanation:

Let suppose that both bus and express train travels at constant speed, whose kinematic formula is now described:

`v = (\Delta s)/(\Delta t)`

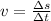
Where:

`v` - Speed, measured in kilometers per hour.

`\Delta s` - Travelled distance, measured in kilometers.

`\Delta t` - Time, measured in hours.

The transportation time is cleared afterwards:

`\Delta t = (\Delta s)/(v)`

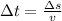
The kinematic expressions for the bus and the express bus are, respectively: (
`\Delta s = 800\,km`)

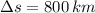Bus

`\Delta t = (800\,km)/(v)`

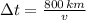
Express train

`\Delta t - 2\,h = (800\,km)/(v + 20\,(km)/(h) )`

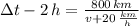
By eliminating
`\Delta t`:

`(800\,km)/(v) -2\,h = (800\,km)/(v+20\,(km)/(h) )`

`(800\,km)/(v) - (800\,km)/(v+20\,(km)/(h) ) = 2\,h`

`800\cdot (v+20)-800\cdot v = 2\cdot v\cdot (v+20)`

`16000 = 2\cdot v^(2)+40\cdot v`

`2\cdot v^(2)+40\cdot v -16000 = 0`

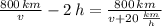
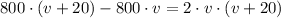
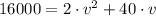
Which is a second-order polynomial and whose roots are:

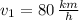`v_(1) = 80\,(km)/(h)` and
`v_(2) = -100\,(km)/(h)`

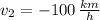
Only first root is physically reasonable, as speed is a scalar, that is, a number that is represented only by magnitude. Then, the time taken by the bus to travel from Central High to Calgary is: (
`v = 80\,(km)/(h)`)

`\Delta t = (800\,km)/(80\,(km)/(h) )`

`\Delta t = 10\,h`

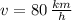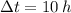
The bus will take 10 hours to travel from South Central High to Calgary.