Answer:
Step 1:
To find ordered pair solutions, you could create an x and y graph and fill out the x side. Then, plug in an x number to get your y number and graph the ordered pairs to see if they give you a straight line. I'm going to use these numbers: -1, 0, 1, and 2.
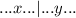
![\left[\begin{array}{ccc}-1&?\\0&?\\1&?\\2&?\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/90bljc9g3qedriufuhis3s5nxsn6bjmmyu.png)
Now, let's plug in -1 into the equation first to see what we get for y.
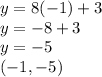
-5 is our y if x was -1.
We do the same for the other three numbers.

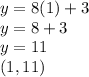

Step 2:
With all that done, we can now fill out our table and graph the points.
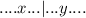
![\left[\begin{array}{ccc}-1&-5\\0&3\\1&11\\2&19\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/yrnhyxwcondstmceuytgrxfqr0ezneqmlc.png)
If you graph these points on graph paper / a graphing website, you will see that these points go in a straight line. If you are given an ordered pair already (for example: (3,5)), then all you have to do is plug in the x into the equation (3) and see if the outcome is true (5).
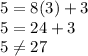
Since they don't equal each other, then (3,5) is false.
Here is the graph for the table above. I hope I helped you!