Question

The mean height of a Clydesdale horse is 72 inches with a standard deviation of 1.2 inches. What is the probability that a Clydesdale is greater than 75 inches tall? Select one: 2.5 0.9938 62.5 0.0062

Answer 1

Answer: 0.0062

Explanation:

We assume that the height of a Clydesdale horse is normally distributed.

Let x denotes the height of the Clydesdale horse

Given: Mean :
`\mu=72\ inches`

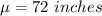
Standard deviation:
`\sigma=1.2\ inches`

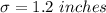
Now, the probability that a Clydesdale is greater than 75 inches tall :

`P(X>75)=P((X-\mu)/(\sigma)>(75-72)/(1.2))\\\\=P(z>2.5)\ \ [z=(X-\mu)/(\sigma)]\\\\=1-P(z\leq2.5)\\\\=1- 0.9937903\ [\text{By z-table}]\\\\=0.0062097\approx0.0062`

Hence, the required probability is 0.0062.