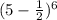Answer:
C.
Explanation:
Given

Required
Determine which binomial expansion it came from
The first step is to add the powers of he expression in brackets;
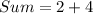
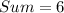
Each term of a binomial expansion are always of the form:

Where n = the sum above
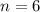
Compare
 to the above general form of binomial expansion
to the above general form of binomial expansion
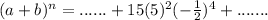
Substitute 6 for n
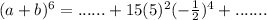
[Next is to solve for a and b]
From the above expression, the power of (5) is 2
Express 2 as 6 - 4
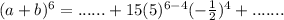
By direct comparison of

and
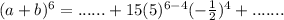
We have;
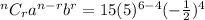
Further comparison gives
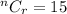
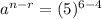

[Solving for a]
By direct comparison of
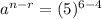
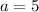
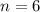
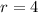
[Solving for b]
By direct comparison of

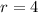
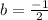
Substitute values for a, b, n and r in

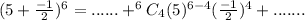
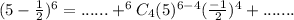
Solve for
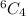
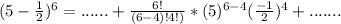
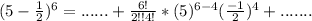
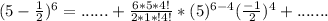

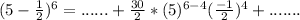
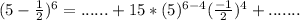

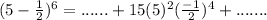
Check the list of options for the expression on the left hand side
The correct answer is