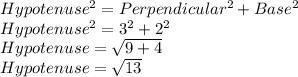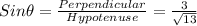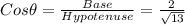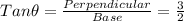Answer:
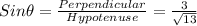
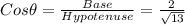
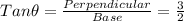
Explanation:
We are given that The point (2, 3) is on the terminal side of angle Θ, in standard position
First Draw a vertical line from the point(2,3) to the x axis.
So, Length of vertical line is 3
The intersection of the line with the x axis is at x=2.
So, now we have obtained a triangle with the horizontal side of length 2, the vertical side of length 3
To Find hypotenuse we will use Pythagoras theorem