Final answer:
The approximate volume of the space between the sphere and the cube is 1308 cubic inches.
Step-by-step explanation:
The volume of a cube with side length 14 inches is calculated by multiplying the length, width, and height:
14 × 14 × 14 = 2744 cubic inches.
The volume of a sphere is calculated using the formula :
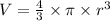 , where r is the radius.
, where r is the radius.
In this case, the diameter of the sphere is equal to the side length of the cube, so the radius is half of the diameter, which is 7 inches. Plugging in the values, the volume of the sphere is approximately :
[tex]V = \frac{4}{3} \times \pi \times 7^3[/tex} = 1436 cubic inches.
To find the approximate volume of the space between the sphere and the cube, subtract the volume of the sphere from the volume of the cube: 2744 - 1436 = 1308 cubic inches.
Therefore, the approximate volume of the space between the sphere and the cube is 1308 cubic inches.