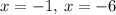Answer:
Explanation:
We can solve this question by applying a quadratic equation, but it would be easier to simply factor the equation. In other words, let's begin by factoring the expression
 + 7x + 6,
+ 7x + 6,
Break this expression down into groups -
 ,
,
Factor out x from "
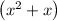 " =
" =
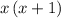 ,
,
Respectively factor out 6 from "
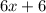 " =
" =
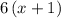 ,
,
 - and now we can group like terms -
- and now we can group like terms -
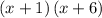
Since we have factored this expression, let's make it equivalent to 0, and solve for x. By the Zero Factor Principle we should receive two solutions,
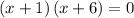 ,
,
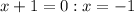 /
/
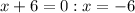 ,
,
The solutions to this equation should thus be :