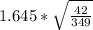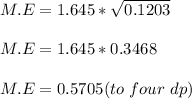Question

Assume that a sample is used to estimate a population proportion p. Find the margin of error E that corresponds to the given statistics and confidence level. Round the margin of error to four decimal places. 95% confidence; n = 349, x = 42

Answer 1

0.5705

Explanation:

Margin of error is expressed as M.E =
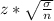`z * \sqrt{(\sigma)/(n) }` where;

z is the z score at 95% confidence

`\sigma` is the standard deviation

n is the sample size

Given n = 349,
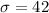`\sigma = 42` and z score at 95% confidence = 1.645

Substituting this values into the formula above we will have;

M.E =
`1.645*\sqrt{(42)/(349) }`

`M.E = 1.645*√(0.1203) \\\\M.E = 1.645*0.3468\\\\M.E = 0.5705 (to\ four\ dp)`