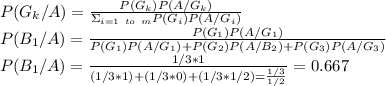Question

There are three cards. One is green on both sides, the second is red on both sides and the third is red on one side and green on the other. We choose a card at random and we see one side (also chosen at random). If the side we see is green, what is the probability that the other side is also green

Answer 1

0.667

Explanation:

According to Bayes theorem:

Since there are three cards, the probability that the side is green = 1/3

For the first card, if one side is green, the probability that the other side is also green = 1 (both sides are green)

For the second card, if one side is green, the probability that the other side is also green = 0 (both sides are red)

For the third card, if one side is green, the probability that the other side is also green = 1/2 (one side is green and the other side is red)

`P(G_k/A)=(P(G_k)P(A/G_k))/(\Sigma_(i=1\ to\ m) P(G_i)P(A/G_i)) \\P(B_1/A)=(P(G_1)P(A/G_1))/(P(G_1)P(A/G_1)+P(G_2)P(A/B_2)+P(G_3)P(A/G_3))\\ P(B_1/A)=(1/3*1)/((1/3*1)+(1/3*0)+(1/3*1/2)=(1/3)/(1/2) )=0.667`