Question

It is nighttime, and you dropped your goggles into a swimming pool that is 3.0m deep. If you hold a laser pointer 1.0m directly above the edge of the pool, you can illuminate the goggles if the laser beam enters the water 2.0m from the edge. How far are the goggles from the edge of the pool

Answer 1

The distance of the goggle from the edge of the pool is 4.726 m

Step-by-step explanation:

The given information are;

The depth of the swimming pool = 3.0 m deep

The height of the laser pointer above the swimming pool edge = 1.0 m

The distance from the pool edge the laser pointer enters the water = 2.0 m

The angle between the pool and the laser = ∅ = tan⁻¹(1/2) = 26.57°

Therefore, the angle of incidence to the vertical
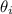`\theta_i`, = θ - ∅ = 90 - 26.57° = 63.43°

By Snell's law we have;

The ratio of the sin of the angle of incidence to the sin of the angle of refraction is a a constant equal to the ratio of the refractive indices as follows;

`(sin (\theta_i))/(sin (\theta_r) =(n_r)/(n_i)`

Where:

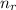`n_r` = Refractive index of the refractive medium which is water = 1.33

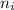`n_i` = Refractive index of the incidence medium which is air = 1.00

Therefore;

`\theta_r = sin^(-1) \left ((n_i * sin (\theta_i))/(n_r) \right) = sin^(-1) \left ((1* sin (63.43))/(1.33) \right) = 42.26 ^(\circ)`

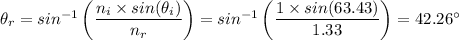
We have that tan(
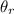`\theta_r`) = (Distance of the goggles from the point directly above the point of incidence of the beam)/(The water depth)

tan(42.26) = (The horizontal distance of the goggles from the point of incidence of the laser on the water surface)/(3.0)

∴ The horizontal distance of the goggles from the point of incidence of the laser on the water surface = 3.0 × tan(42.26) = 2.726 m

The distance of the goggle from the edge of the pool = The horizontal distance of the goggles from the point of incidence of the laser on the water surface + The distance from the edge of the water surface the laser enters the water

The distance of the goggle from the edge of the pool = 2.726 + 2 = 4.726 m

The distance of the goggle from the edge of the pool = 4.726 m.