Question

Your client, Bo Regard, holds a complete portfolio that consists of a portfolio of risky assets (P) and T-Bills. The information below refers to these assets. What is the expected return on Bo's complete portfolio?

Answer 1

The expected return on Bo's complete portfolio will be "10.32%".

Step-by-step explanation:

The given question is incomplete. Please find attachment of the complete question.

According to the question, the given values are:

Port's expected return,

`R_p=12 \ percent`

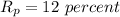
T-bill's expected return,

`R_t=3.6 \ percent`

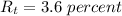
Port's weight,

`W_p=80 \ percent \ i.e.,\ 0.80`

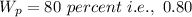
T-bill's weight,

`W_t=20 \ percent \ i.e., \ 0.20`

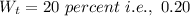
Now,

The Bo's complete portfolio's expected return will be:

⇒
`W_p* R_p+W_t* R_t`

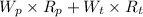
On substituting the given values, we get

⇒
`0.80* 12 \ percent+0.20* 3.6 \ percent`

⇒
`10.32 \ percent`

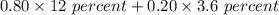
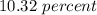
Note: percent = %