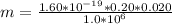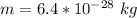Question

In a mass spectrometer, a single-charged particle (charge e) has a speed of 1.0 × 10 6 m/s and enters a uniform magnetic field of 0.20 T. The radius of the circular orbit is 0.020 m. What is the mass of the particle?

Answer 1

The mass is
`m =6.4*10^(-28) \ kg`

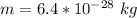
Step-by-step explanation:

From the question we are told that

The speed of the charge is
`v = 1.0 *10^(6) \ m/s`

The magnetic field is
`B = 0.20 \ T`

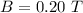
The radius is
`r = 0.02 \ m`

The value of the charge is
`e = 1.60 *10^(-19) \ C`

The centripetal acting on the charge moving in the circular orbit is mathematically represented as

`F_c = (mv^2)/(r )`

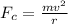
Now this centripetal force is due to the force exerted on the charge by the magnetic field on the charge which is mathematically represented as

`F_m = qv B sin\theta`

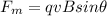
At the maximum of this magnetic force
`\theta = 90 ^o`

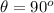
So

`F_m = e v B sin(90)`

`F_m = e v B`

Now given that it is this magnetic force that is causing the circular motion we have that

`F_c = F_m`

=>
`(mv^2)/(r ) = ev B`

=>
`m = (e * B * r )/(v )`

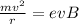
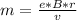
substituting values

`m = ( 1.60 *10^(-19) * 0.20 * 0.020 )/(1.0*10^(6) )`

`m =6.4*10^(-28) \ kg`