In an arithmetic sequence, consecutive terms differ by a fixed number d :
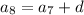
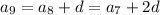
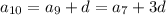
and so on up to

Solve for d :
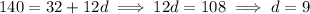
Work backwards to find the first term in the sequence, and hence the n-th term:
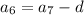
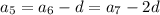
and so on down to
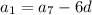
So the first term is
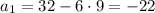
which means the n-th term is
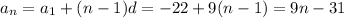
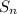 denotes the n-th partial sum of the sequence, i.e. the sum of the first n terms. We want to find the number of terms such that this sum is 511:
denotes the n-th partial sum of the sequence, i.e. the sum of the first n terms. We want to find the number of terms such that this sum is 511:
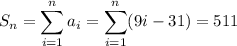
Distribute the summation and recall the formulas,
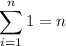
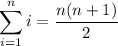

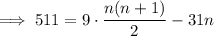
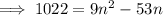
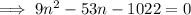
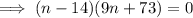
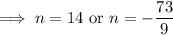
n must be a positive integer, so we the sum is obtained from the first n = 14 terms.