Answer:
4773 peoples.
Explanation:
Given the number of people d, in thousands applying for medical benefits per week in a particular city c modeled by the equation d(t)=2.5 sin(0.76t+0.3)+3.8 where t is the time in years, the maximum number of people tat will apply will occur at d(t)/dt = 0
Differentiating the function given with respect to t, we will have;
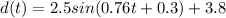
First we need to know that differential of any constant is zero.

If
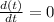 then;
then;
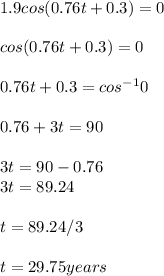
To know the maximum number of people in thousands that apply for benefits per year in the city, we wil substitute the value of t = 29.75 into the modeled equation

Since d is in thousands, the maximum number of people in thousands will be 4.7732*1000 = 4773.2 which is approximately 4773 peoples.