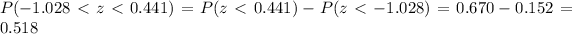Question

A certain car model has a mean gas mileage of 34 miles per gallon (mpg) with a standard deviation A pizza delivery company buys 54 of these cars. What is the probability that the average mileage of the fleet is between 33.3 and 34.3 mpg?

Answer 1

`z =(33.3- 34)/((5)/(√(54)))= -1.028`

`z =(34.3- 34)/((5)/(√(54)))= 0.441`

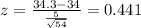
An we can use the normal standard table and the following difference and we got this result:

`P(-1.028<z<0.441)= P(z<0.441) -P(z<-1.028) = 0.670 -0.152 =0.518`

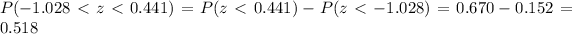
Explanation:

Assuming this statement to complete the problem "with a standard deviation 5 mpg"

We have the following info given:

`\mu = 34` represent the mean

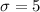`\sigma= 5` represent the deviation

We have a sample size of n = 54 and we want to find this probability:

`P(33.3 < \bar X< 34.3)`

And for this case since the sample size is large enough >30 we can apply the central limit theorem and then we can use this distribution:

`\bar X \sim N(\mu , (\sigma)/(√(n)))`

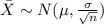
And we can use the z score formula given by:

`z=(\bar X -\mu)/((\sigma)/(√(n)))`

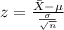
And replacing we got:

`z =(33.3- 34)/((5)/(√(54)))= -1.028`

`z =(34.3- 34)/((5)/(√(54)))= 0.441`

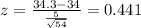
An we can use the normal standard table and the following difference and we got this result:

`P(-1.028<z<0.441)= P(z<0.441) -P(z<-1.028) = 0.670 -0.152 =0.518`