Question

The pressure applied to a leverage bar varies inversely as the distance from the object. If 150 pounds is required for a distance of 10 inches from the object how much pressure is needed for a distance of 3 inches

Answer 1

500 pounds

Explanation:

Let the pressure applied to the leverage bar be represented by p

Let the distance from the object be represented by d.

The pressure applied to a leverage bar varies inversely as the distance from the object.

Written mathematically, we have:

`p \propto (1)/(d)`

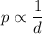
Introducing the constant of proportionality

`p = (k)/(d)`

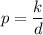
If 150 pounds is required for a distance of 10 inches from the object

• p=150 pounds
• d=10 inches

`150 = (k)/(10)\\\\k=1500`

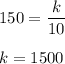
Therefore, the relationship between p and d is:

`p = (1500)/(d)`

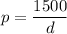
When d=3 Inches

`p = (1500)/(3)\\\implies p=500$ pounds`

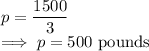
The pressure applied when the distance is 3 inches is 500 pounds.