Question

If the ratio of the surface areas of two similar geometrical solids is given by 121:36, what is the

ratio of their volumes?

Answer 1

1331:216

Explanation:

Given the ratio of the lengths of two similar solids as a:b

The ratio of the surface areas =
`a^2:b^2`

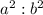
The ratio of the volume =
`a^3:b^3`

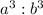
We are given that the ratio of the surface areas of two similar geometrical solids is given by 121:36

Therefore:

`a^2:b^2=121:36\\\implies a^2:b^2=11^2:6^2\\\implies a:b=11:6`

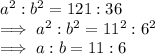
Since the ratio of the lengths is 11:6

The ratio of their volumes =
`11^3:6^3`

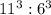
=1331:216

The ratio of the volume of the two similar geometrical solids is 1331:126.