Question

Una compañía sabe que si produce "x" unidades mensuales su utilidad "u" se podría calcular con la expresión: u(x)=-0.04x^2+44x-4000 donde "u" se expresa en dólares. Determine la razón del cambio promedio de la utilidad cuando el nivel de producción cambia de 600 a 620 unidades mensuales. Recuerde que la pendiente de la recta secante a la gráfica de la función representa a la razón de cambio promedio.

Answer 1

The ratio of the average change in profit when the level of production changes from 600 to 620 units per month is -24 : 5.

Explanation:

The question is:

A company knows that if it produces "x" monthly units its utility "u" could be calculated with the expression: u (x) = - 0.04x ^ 2 + 44x-4000 where "u" is expressed in dollars. Determine the ratio of the average change in profit when the level of production changes from 600 to 620 units per month. Remember that the slope of the secant line to the graph of the function represents the average rate of change.

Solution:

The expression for the utility is:

`u (x) = - 0.04x ^ {2} + 44x-4000`

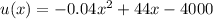
It is provided that the slope of the secant line to the graph of the function represents the average rate of change.

Then the ratio of the average change in profit when the level of production changes is:

`\text{Average change in profit}=(u(x_(2))-u(x_(1)))/(x_(2)-x_(1))`

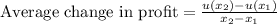
Compute the values of u (x₁) and u (x₂) as follows:

x₁ = 600

`u (x_(1)) = - 0.04x_(1) ^ {2} + 44x_(1)-4000`

`= - 0.04(600) ^ {2} + 44(600)-4000\\=-14400+26400-4000\\=8000`

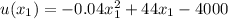
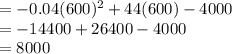
x₂ = 620

`u (x_(2)) = - 0.04x_(2) ^ {2} + 44x_(2)-4000`

`= - 0.04(620) ^ {2} + 44(620)-4000\\=-15376+27280-4000\\=7904`

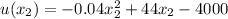
Compute the average rate of change as follows:

`\text{Average change in profit}=(u(x_(2))-u(x_(1)))/(x_(2)-x_(1))`

`=(7904-800)/(620-600)\\\\=(-96)/(20)\\\\=-(24)/(5)\\\\=-24:5`

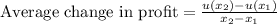
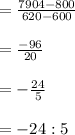
Thus, the ratio of the average change in profit when the level of production changes from 600 to 620 units per month is -24 : 5.