Question

Two vectors are said to be parallel if they point in the same direction or if they point in opposite directions.

Part A
Are the vectors v1 = < V3, 1 >and va = <-13, -1 >parallel? Show your work and explain
Part B
Are the vectors Ui =< 2, 3 >and u2 =-3,-2 > parallel? Show your work and explain.
​

Answer 1

When two vectors are parallel, it's because the angles of inclination are equivalent. They are defined by

`\theta = tan^(-1)((y)/(x) )`

So, we just need to find the angle for each vector and see if they are equivalent.

We have vectors
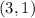`(3,1)` and
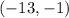`(-13,-1)`. You already can deduce that these vectors are not parallel, because, their divisions are not equivalent.

`(1)/(3) \\eq (-1)/(-13)`

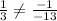
Which will give different angles in the end.

Let's try the other pair of vectors
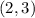`(2,3)` and
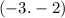`(-3.-2)`. Their division would be

`(3)/(2) \\eq (-2)/(-3)\\ 1.5 \\eq 0.67`

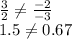
As you can observe, their divisions are not equivalent, which means their tangents are not equivalent.

Therefore, those vectors are not parallel, because they don't have equivalent angles of inclination, not matter if they are pointing to the same or different direction.