Given Information:
Launch angle of projectile = 30°
Initial velocity = V₀ = 30 m/s
Acceleration due to gravity = g = 10 m/s²
Required Information:
Angle with the horizontal after 1.5 sec = ?
Answer:
The angle of the projectile to the horizontal after t = 1.5 seconds is 0°
Explanation:
The horizontal component of the velocity is given by
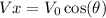
Where V₀ is the initial velocity and θ is the launch angle
The vertical component of the velocity is given by
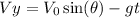
Where V₀ is the initial velocity, θ is the launch angle, g is the acceleration due to gravity and t is the time.
So after t = 1.5 sec
The horizontal component of the velocity is
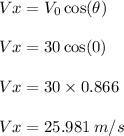
And the vertical component of the velocity is
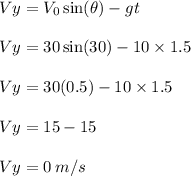
The angel is

Therefore, the angle of the projectile to the horizontal after t = 1.5 seconds is 0°