Question

A recent national survey found that high school students watched an average (mean) of 7.8 movies per month with a population standard deviation of 0.5. The distribution of number of movies watched per month follows the normal distribution. A random sample of 30 college students revealed that the mean number of movies watched last month was 7.3. At the 0.05 significance level, can we conclude that college

Answer 1

Explanation:

Given that :

Mean = 7.8

Standard deviation = 0.5

sample size = 30

Sample mean = 7.3 5.4772

The null and the alternative hypothesis is as follows;

`\mathbf{ H_o: \mu \geq 7.8}`

`\mathbf{ H_1: \mu < 7.8}`

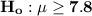
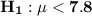
The test statistics can be computed as :

`z = (X- \mu)/((\sigma)/(√(n)))`

`z = (7.3- 7.8)/((0.5)/(√(30)))`

`z = (-0.5)/((0.5)/(5.4772))`

`z = - 5.4772`

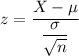
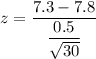
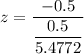
The p-value at 0.05 significance level is:

p-value = 1- P( Z < -5.4772)

p value = 0.00001

Decision Rule:

The decision rule is to reject the null hypothesis if p value is less than 0.05

Conclusion:

At the 0.05 significance level, there is sufficient information to reject the null hypothesis. Therefore ,we conclude that college students watch fewer movies a month than high school students.