Question

In a survey of 300 T.V. viewers, 40% said they watch network news programs. Find the margin of error for this survey if we want 95% confidence in our estimate of the percent of T.V. viewers who watch network news programs.

Answer 1

0.05543

Explanation:

The formula for calculating the margin of error is expressed as;

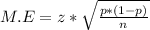`M.E = z * \sqrt{(p*(1-p))/(n) }` where;

z is the z-score at 95% confidence = 1.96 (This is gotten from z-table)

p is the percentage probability of those that watched network news

p = 40% = 0.4

n is the sample size = 300

Substituting this values into the formula will give;

`M.E = 1.96*\sqrt{(0.4(1-0.4))/(300) }\\ \\M.E = 1.96*\sqrt{(0.4(0.6))/(300) }\\\\\\M.E = 1.96*\sqrt{(0.24)/(300) }\\\\\\M.E = 1.96*√(0.0008)\\\\\\M.E = 1.96*0.02828\\\\M.E \approx 0.05543`

Hence, the margin of error for this survey if we want 95% confidence in our estimate of the percent of T.V. viewers who watch network news programs is approximately 0.05543