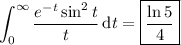I'm guessing your supposed to compute the value of the integral
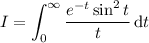
by way of Laplace transform.
The integral is equivalent to the transform of
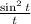 when
when
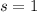 , since
, since
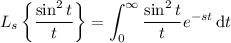
Recall the frequency-domain integration property of the transform:
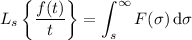
where
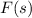 is the Laplace transform of
is the Laplace transform of
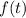 .
.
Let
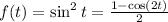 ; then
; then
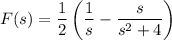
Next, it follows that
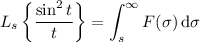
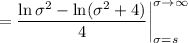
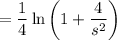
Get the value of
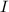 by substituting
by substituting
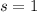 :
: