Answer:
Pyramid
Explanation:

Given that the two solids have the same volume
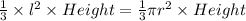
If the length of a side of the square base of pyramid A is the same as the base radius of cone B. i.e l=r
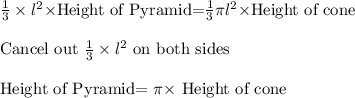
If the height of the cone is 1

Therefore, the pyramid has a greater height.