Question

A polynomial has a leading coefficient of 1 and the

following factors with multiplicity1:
x-(2 + i)
X - V2
What is the factored form of the polynomial?

Answer 1

A

Explanation:

EDGE 2021

Answer 2

(A)
`[x-(2+i)][x-(2-i)][x-√(2)][x+√(2)]`

Explanation:

A polynomial has a leading coefficient of 1 and the following factors with multiplicity 1:

`x-(2+i)\\x-√(2)`

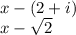
We apply the following to find the factored form of the polynomial.

• If a complex number is a root of a polynomial with real coefficients, its complex conjugate is also a root of that polynomial.

• If the polynomial has an irrational root
  `a+√(b)`, where a and b are rational and b is not a perfect square, then it has also a conjugate root
  `a-√(b)`.

`\text{Complex conjugate of }x-(2+i)=x-(2-i)\\\\\text{Complex conjugate of }x-√(2)=x+√(2)`

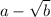Therefore, the factored form of the polynomial is:

`[x-(2+i)][x-(2-i)][x-√(2)][x+√(2)]`