Question

A fruit company has 20% returns in periods of normal rainfall and -3% returns in droughts. The probability of normal rainfall is 60% and droughts 40%. What would the fruit company’s expected returns be?

Answer 1

`E(x) = 10.8\% \\\\`

The fruit company’s expected returns are 10.8%

Step-by-step explanation:

The expected returns of the fruit company is given by

`E(x) =\sum (x \cdot P(x)) \\\\`

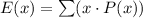
For the given case,

Returns in normal rainfall = x₁ = 20% = 0.20

Returns in drought = x₂ = -3% = -0.03

Probability of normal rainfall = P(x₁) = 60% = 0.60

Probability of drought = P(x₂) = 40% = 0.40

So, the expected value of returns is

`E(x) = x_1 \cdot P(x_1) + x_2 \cdot P(x_2) \\\\E(x) = 0.20 \cdot 0.60 - 0.03 \cdot 0.40 \\\\E(x) = 0.12 - 0.012 \\\\E(x) = 0.108 \\\\E(x) = 10.8\% \\\\`

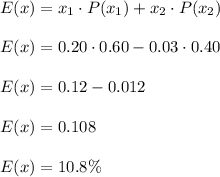
Therefore, the fruit company’s expected returns are 10.8%