Question

Help me fast please

give the coordinates of the
foci,vertices,and convertices of the ellipse with equation x²/169 + y²/25 = 1​​

Answer 1

We can see that for this case the vertex is
`V= (0,0)`

The values for a and b are:

`a = √(169)=13, b= √(25)=1`

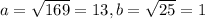
Then the ellipse have the major axis on x.

In order to find the two foci we need to use the following formula:

`c =√(a^2 -b^2)`

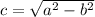
And replacing we got:

`c =√(169-25)= \pm 12`

And then the two foci are (12,0) and (-12,0)

And the covertex are on this case (-13,0) (13,0) and (0,5) (0,-5) on the y axis

Explanation:

For this problem we have the following equation given:

`(x^2)/(169) + (y^2)/(25)= 1`

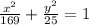
If we compare this with the general expression of an ellipse given by:

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)= 1`

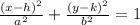
We can see that for this case the vertex is
`V= (0,0)`

The values for a and b are:

`a = √(169)=13, b= √(25)=1`

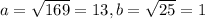
Then the ellipse have the major axis on x.

In order to find the two foci we need to use the following formula:

`c =√(a^2 -b^2)`

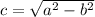
And replacing we got:

`c =√(169-25)= \pm 12`

And then the two foci are (12,0) and (-12,0)

And the covertex are on this case (-13,0) (13,0) and (0,5) (0,-5) on the y axis