Answer:
They will find 69 viruses in 8 hours.
Explanation:
The number of viruses after t hours is given by the following equation:

In which V(0) is the initial number of viruses and r is the decay rate, as a decimal.
They start with 500 viruses
This means that

Decay rate of 22% per hour.
This means that
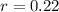
So

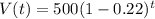
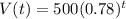
How many viruses will they find in 8 hours?
This is V(8).
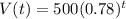
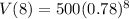
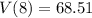
Rounding to the nearest whole number
They will find 69 viruses in 8 hours.