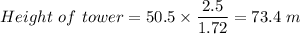Question

A pole that is 2.5 M tall cast a shadow that is 1.72M lawn dart at the same time a nearby tower cast a shadow that is 50.5 M long how tall is the tower round answer to the nearest meter

Answer 1

The tower is 73.4 m tall

Explanation:

The height of the pole = 2.5 m

The shadow cast by the pole = 1.72 m

Shadow cast by tower = 50.5 m

To find the height of the tower, we proceed by finding the angle of elevation, θ, of the light source casting the shadows as follows;

`Tan\theta =(Opposite \ side \ to\ angle \ of \ elevation)/(Adjacent\ side \ to\ angle \ of \ elevation) = (Height \ of \ pole )/(Length \ of \ shadow) =(2.5 )/(1.72)`

`\theta = tan ^(-1) \left ((2.5 )/(1.72) \right) = 55.47 ^(\circ)`

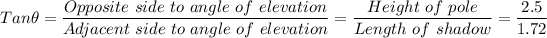
The same tanθ gives;

`Tan\theta = (Height \ of \ tower)/(Length \ of \ tower \ shadow) =(Height \ of \ tower )/(50.5) = (2.5)/(1.72)`

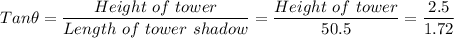
Which gives;

`{Height \ of \ tower } = {50.5} * (2.5)/(1.72) = 73.4 \ m`