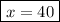Question

What is the value of x? A.20 B.40 C.45 D.85

Answer 1

40°

Option B is the correct option.

Explanation:

The sum of complementary angles = 90°

Now, Let's find the value of X

`2x + 10 = 90`

Move constant to R.H.S and change its sign

`2x = 90 - 10`

Calculate the difference

`2x = 80`

Divide both sides of the equation by 2

`(2x)/(2) = (80)/(2)`

Calculate

`x = 40`

Hope this helps...

Best regards!

Answer 2

`\boxed{x = 40}`

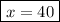
Explanation:

Part 1: Determining the type of angles that need solved

First, we need to look at the angles provided to notice a key detail -- they add up to make a 90 degree angle. Therefore, we can just add the two values together, set them equal to 90, and solve for x.

Part 2: Setting up an equation

Now, using the information we just retrieved, we need to set up an equation for us to solve:

`10 + 2x = 90`

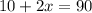
Part 3: Solving the equation

Finally, just solve for x:

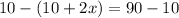`10 - (10 + 2x) = 90 - 10` Subtract 10 from both sides to isolate the variable and its coefficient.

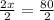`(2x)/(2) = (80)/(2)` Divide by 2 on both sides to isolate the variable.

`\boxed{x = 40}`