Question

A culture started with 5,000 bacteria. After 2 hours, it grew to 6,000 bacteria. Predict how many bacteria will be present after 14 hours. Round your answer to the nearest whole number. P=ae^kt

Answer 1

There will be approximately 17915 bacteria after 14 hours.

Explanation:

Assuming that the bacteria are growing at a exponential rate expressed by the formula:

`P = 5000*e^(k*t)`

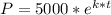
Where 5000 is the initial number of bacteria and t is the time elapsed in hours, we first need to find the value of k. This is done by applying a known point to the function, which would be 2 hours after the start in this case.

`6000 = 5000*e^(k*2)\\e^(2*k) = 1.2\\ln(e^(2*k)) = ln(1.2)\\2*k = ln(1.2)\\k = (ln(1.2))/(2) = 0.09116`

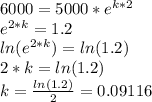
We can now predict the number of bacteria after 14 hours as shown below:

`P = 5000*e^((0.09116*14)) = 5000*e^((1.27624))\\P = 17915.7`

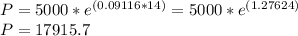
There will be approximately 17915 bacteria after 14 hours.