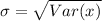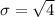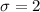Question

Suppose that the probability distribution below shows the number of colleges that children of celebrities applied to in 2018. Compute the standard deviation for the number of college applications.

x 0 2 4 6
P(x) 0.4 0.3 0.2 0.1

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The standard deviation is
`\sigma = 2.45`

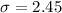
Explanation:

From the given data we can compute the expected mean for each random values as follows

`E(X) = \sum [ X * P(X = x )]\\\\ X \ \ \ \ \ \ X* P(X =x )\\ 0 \ \ \ \ \ \ \ \ \ \ 0* 0.4 = 0 \\ 2 \ \ \ \ \ \ \ \ \ \ 2 * 0.3 = 0.6 \\ 4 \ \ \ \ \ \ \ \ \ \ 4 * 0.2 = 0.8\\ 6 \ \ \ \ \ \ \ \ \ \ 6* 0.1 = 0.6`

So

`E(x) = 0 + 0.6 + 0.8 + 0.6`

`E(x) = 2`

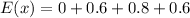
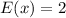
The

`E(X^2) = \sum [ X^2 * P(X = x )]\\\\ X \ \ \ \ \ \ \ \ \ \ X^2 * P(X=x ) \\ 0 \ \ \ \ \ \ \ \ \ \ 0^2 * 0.4 = 0 \\ 2 \ \ \ \ \ \ \ \ \ \ 2^2 * 0.3 = 12 \\ 4 \ \ \ \ \ \ \ \ \ \ 4^2 * 0.2 = 3.2 \\ 6 \ \ \ \ \ \ \ \ \ \ 6^2 * 0.1 = 3.6`

So

`E(X^2) = 0 + 1.2 + 3.2 + 3.6`

`E(X^2) = 8`

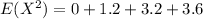
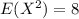
Now the variance is mathematically evaluated as

`Var (X) = E(X^2 ) -[E(X]^2`

Substituting value

`Var (X) = 8-4`

`Var (X) = 6`

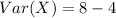
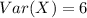
The standard deviation is mathematically evaluated as

`\sigma = √(Var(x))`

`\sigma = √(4)`

`\sigma = 2`