Question

A bond currently has a price of $1,050. The yield on the bond is 7%. If the yield increases 23 basis points, the price of the bond will go down to $1,037. The duration of this bond is ____ years.

Answer 1

The duration of the bond is 5.8 years

Step-by-step explanation:

Given that :

Current price of a bond $1,050

Yield on the bond = 7% = 0.07

If the yield increases 23 basis points, the price of the bond will go down to $1,037

The objective is to determine the duration of the bond.

In order to determine the duration of the bond; we need to first find the change in percentage of the price. Afterwards, this is find the modified duration which quantify the change in percentage in the market price for every change in the yield to maturity. Then finally to the determination of the duration of the bond.

Mathematically;

Percentage change in price =
`(new \ price - old \ price )/(old \ price)`

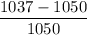
Percentage change in price =
`(1037 - 1050 )/(1050)`

Percentage change in price =
`(-13 )/(1050)`

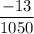
Percentage change in price = −0.01238

Percentage change in price ≅ - 0.0124

Percentage change in price = - 1.24%

Let recall from the knowledge of our basis points which say;

1 basis point = 1/100

Therefore ; given that if he yield increases 23 basis points, then we have:

23 basis point = 23/100 = 0.23

The modified duration =
`(percentage \ change \ in \ price )/( change)`

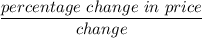
The modified duration =
`(1.24 )/(0.23)`

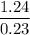
The modified duration = 5.3913 years

Finally, The duration of the bond = Modified duration × (1 + Yield to Maturity)

The duration of the bond = 5.3913 × (1 + 0.07)

The duration of the bond = 5.3913 × 1.07

The duration of the bond = 5.768691 years

The duration of the bond ≅ 5.8 years