Fifty students are enrolled in a Business Statistics class. After the first examination, a random sample of 5 papers was selected. The grades were 60, 75, 80, 70, and 90. a) Det…

Question

asked Mar 3, 2021 27.1k views

1 Answer

Ozooxo · Answer 1 · 2021-03-08T12:33:42+0000

Answer:

The standard error S.E of the mean is 5

Explanation:

From the given data;

Fifty students are enrolled in a Business Statistics class.

After he first examination, a random sample of 5 papers was selected.

Now; let consider a random sample of 5 papers was selected. with the following grades : 60, 75, 80, 70, and 90

The objective of this question is to determine the standard error of the mean

In order to achieve this ; we need to find the mean and the standard deviation from the given data.

TO start with the mean;

Mean
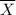$\overline X$ =
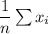
$(1)/(n) \sum x_i$

Mean
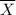$\overline X$ =
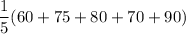
(1)/(5) (60+75+80+70+90)

Mean
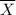$\overline X$ = 0.2(375)

Mean
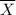$\overline X$ = 75

On the other hand; the standard deviation is :

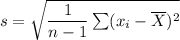
$s = \sqrt{(1)/(n-1)\sum(x_i - \overline X)^2}$

$s = \sqrt{(1)/(5-1)((60-75)^2+(75-75)^2+(80-75)^2+(70-75)^2+(90-75)^2 )}$

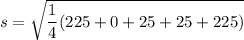
$s = \sqrt{(1)/(4)(225+0+25+25+225 )}$

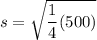
$s = \sqrt{(1)/(4)(500 )}$

s = √(125)

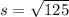
s = 11.18

Finally; the standard error S.E of the mean is:

S.E = (s)/(√(n))

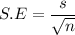
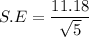
S.E = (11.18)/(√(5))

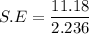
S.E = (11.18)/(2.236)

S.E = 5

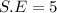
The standard error S.E of the mean is 5