Question

Safegate Foods, Inc., is redesigning the checkout lanes in its supermarkets throughout the country and is considering two designs. Tests on customer checkout times conducted at two stores where the two new systems have been installed result in the following summary of the data.

System System B
n1=120 n2=100
x1=4.1 minutes x2=3.4 minutes
σ1=2.2minutes σ2= 1.5 minutes

Test at the 0.05 level of significance to determinewhether the population mean checkout times of the two newsystems differ. Which system is preferred?

Answer 1

We conclude that the population means checkout times of the two new systems differ.

Explanation:

We are given the result in the following summary of the data;

System System B

n1=120 n2=100

x1=4.1 min x2=3.4 min

σ1=2.2 min σ2= 1.5 min

Let
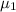`\mu_1` = population mean checkout time of the first new system

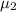`\mu_2` = population mean checkout time of the second new system

So, Null Hypothesis,
`H_0` :
`\mu_1=\mu_2` {means that the population mean checkout times of the two new systems are equal}

Alternate Hypothesis,
`H_A` :
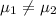`\mu_1\\eq \mu_2` {means that the population mean checkout times of the two new systems differ}

The test statistics that will be used here is Two-sample z-test statistics because we know about population standard deviations;

T.S. =
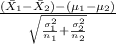`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{\sqrt{(\sigma_1^(2) )/(n_1) + (\sigma_2^(2) )/(n_2)} }` ~ N(0,1)

where,
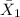`\bar X_1` = sample mean checkout time of the first new systems = 4.1 min

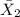`\bar X_2` = sample mean checkout time of the second new systems = 3.4 min

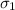`\sigma_1` = population standard deviation of the first new systems = 2.2 min

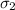`\sigma_2` = population standard deviation of the second new systems = 1.5 min

`n_1` = sample of the first new systems = 120

`n_2` = sample of the second new systems = 100

So, the test statistics =
`\frac{(4.1-3.4)-(0)}{\sqrt{(2.2^(2) )/(120) + (1.5^(2) )/(100)} }`

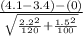
= 2.792

The value of z-test statistics is 2.792.

Now, at 0.05 level of significance, the z table gives a critical value of -1.96 and 1.96 for the two-tailed test.

Since the value of our test statistics does not lie within the range of critical values of z, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the population mean checkout times of the two new systems differ.