Answer:
Moment of inertia of the flywheel is equal to 10.19 kg-m^2
Step-by-step explanation:
The maximum rotational energy to be stored by the flywheel
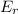 = 2.00 x 10^6 J
= 2.00 x 10^6 J
Angular speed with which to store this energy ω = 443 rad/s
moment of inertia of the flywheel
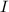 = ?
= ?
Recall that the energy of a rotating body is gotten from the equation
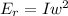
Where
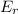 is the rotational energy of the rotating body
is the rotational energy of the rotating body
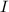 = moment of inertia of the body
= moment of inertia of the body
ω = angular speed of the rotating body
imputing the values into the equation, we'll have
2.00 x 10^6 =
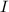 x
x
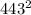
2.00 x 10^6 =
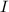 x 196249
x 196249
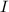 = (2.00 x 10^6) ÷ 196249 = 10.19 kg-m^2
= (2.00 x 10^6) ÷ 196249 = 10.19 kg-m^2