Question

What must be the first cost of Alternative B to make the two alternatives equally attractive economically at an interest rate of 8% per year

Answer 1

The answer is "21,622.98".

Step-by-step explanation:

In the given question some information is missing, which can be defined in the given attachment.

To calculate the first cost we first subtract B cost is to X.

NPV = Cash Flow of the sum of PV amount

`PV = \frac{Flow of cash} {(1+i)^n} \\\\ \ Calculating \ the \ NPV \ of \ option \ A: \\\\`

`= (-16600)/((1 + 0.08)^0)-(2400)/((1 + 0.08)^1)-(2400)/((1 + 0.08)^2) -(2400)/((1 + 0.08)^3)-(2400)/((1 + 0.08)^4)`

`= (-16600)/(1)-(2400)/(1.08)-(2400)/(1.16)-(2400)/(1.25)-(2400)/(1.36)`

`=-16600-2222.22-2068.96-1920-1764.70\\\\=-24,575.88`

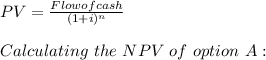
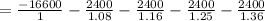
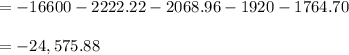
The value of Option A or NPV = -24,575.88

The value of Option B or NPV:

`=-(X)/((1 + 0.80)^0)-(1000)/((1 + 0.08)^1) -(1000)/((1 + 0.08)^2)-(1000)/((1 + 0.08)^3)-(1000)/((1 + 0.08)^4) \\\\ =-(X)/((1.80)^0)-(1000)/((1.08)^1) -(1000)/((1.08)^2)-(1000)/((1.08)^3)-(1000)/((1.08)^4)`

`= -(X)/(1)-(1000)/(1.08)-(1000)/(1.16)-(1000)/(1.25)-(1000)/(1.36)\\\\= -X -555.55-862.06-800-735.29\\\\=-X -2952.9`

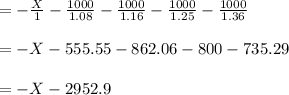
The value of Option B or NPV = -X -2952.9

As demanded

In Option B the value of NPV = In Option A the value of NPV

`-X -2952.9= -24,575.88\\\\-X= -21,622.98\\\\X=21,622.98\\`