Answer:
V=34.2 m/s
Step-by-step explanation:
Given that
Height , h= 54 m
Horizontal distance , x = 35 m
Given that , the ball is thrown horizontally , therefore the initial vertical velocity will be zero.
In vertical direction :
We know that
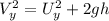
Now by putting the values in the above equation we got
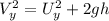
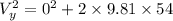
Assume
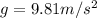
Thus
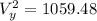

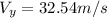
We also know that
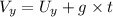
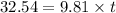
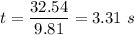
In horizontal direction :
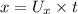
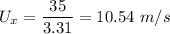
Thus the resultant velocity
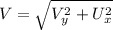
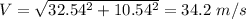
V=34.2 m/s
Therefore the velocity will be 34.2 m/s.